Test Your Knowledge
What Are Acids and Bases?
1. Which of the following bases satisfy the definition proposed by Brønsted and Lowry but do not satisfy the definition proposed by Arrhenius?I. Mg(OH)2
II. CH3CH2COO-
III. NaOH
IV. C5H5N
a) I and II
b) II and III
c) II and IV
d) IV
e) None of the above
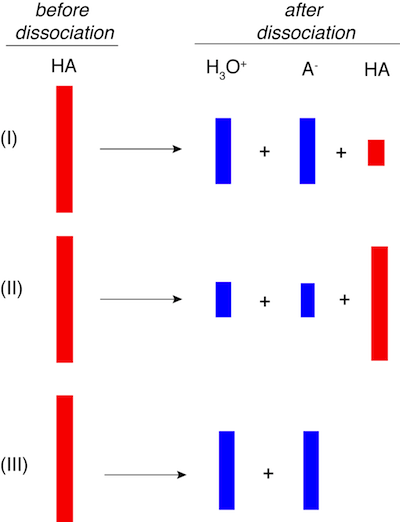
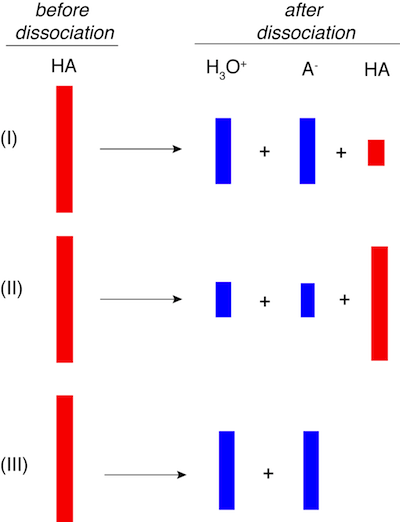
2. If the red boxes below represent an acid before dissociation into the blue boxes representing product concentrations, which of the three scenarios depicts the weakest acid?
3. Label the conjugate acid-base pairs in the following chemical equation:
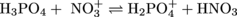
4. Assuming equal concentrations of reactants and products, will the following acid-base reaction proceed to the right or to the left?
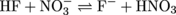
5. The following reaction can be viewed as a Lewis acid-base reaction. Which molecule is acting as a Lewis acid and which is acting as a Lewis base?
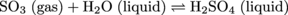
Water as an Acid and Base
1. If the concentration of H3O+ in a solution at 25 °C is 2.5 × 10-5 M, what is the concentration of OH-?a) 3 × 10-5 M
b) 1 × 10-7 M
c) 0
d) 1 × 10-14 M
e) 4 × 10-10 M
2. The solution above is ______ .
a) lacking a conjugate base
b) basic
c) acidic
d) neutral
e) lacking a conjugate base
3. At 60 °C the value of Kw increases from its value at 25 °C. The Kw value at 60 °C is 1.3 × 10-13. If the concentration of OH- in a solution at 60 °C is 3.6 × 10-7 M, what is the concentration of H3O+?
a) 1.3 × 10-6 M
b) 1 × 10-7 M
c) 3.6 × 10-7 M
d) 1.3 × 10-13 M
e) 1.3 × 10-7 M
4. The solution above is _______ .
a) neutral at 25 °C and neutral at 60 °C
b) basic
c) acidic at 25 °C and neutral at 60 °C
d) basic at 25 °C and neutral at 60 °C
e) acidic
5. What is the value for Kw if a neutral solution contains 1 × 10-6 M of H3O+?
a) 1 × 10-14
b) 1 × 10-7
c) It's not possible to have a neutral solution with [H3O+] = 1 × 10-6 M H3O+.
d) 1 × 10-12
e) 2 × 10-14
pH: Definition and Measurement
1. What is the pH of a solution at 25 °C that has an OH- concentration of 2.8 × 10-4 M?a) 7.00
b) 2.80
c) 11.20
d) 10.45
e) 9.15
2. What is the pH of a solution at 100 °C that has a H3O+ concentration of 7.16 × 10-7 M?
a) 6.14
b) 5.14
c) 7.85
d) 7.00
e) 8.35
3. The solution in question 2 is _________. (Note that Kw at 100 °C is 51.3 × 10-14).
a) acidic
b) basic
c) neutral
d) unrealistic
e) likely frozen solid
4. A solution has a pOH of 10.20 at 25 °C. What is the H3O+ concentration of this solution?
a) 6.3 × 10-11 M
b) 1.6 × 10-4 M
c) 3.80 M
d) negligible
e) 1.8 × 10-4 M
5. Pretend you want to measure the pH of a solution that you suspect is in the ballpark of pH 7.5. Which of the following acid-base indicators would you want to use? (Values in parentheses are the pH at which 50% of the indicator is in the protonated form and 50% is in the deprotonated form).
a) methyl violet (0.8)
b) methyl orange (3.47)
c) bromocresol green (4.7)
d) phenol red ( 7.7)
e) alizarin yellow (11.0)
The Equilibria of Acids-Base Solutions
1. What is the pH of a 1.00 × 10-4 M solution of Ba(OH)2 solution (at 25 °C)?a) 10.0
b) 10.3
c) 3.7
d) 4
e) 12.3
2. If the red boxes below represented an acid before dissociation into the blue boxes representing product concentrations, list the acids in order of increasing Ka value.
3. What is the percent dissociation of a 0.10 M solution of HNO2, which has a pKa value of 3.29 (at 25 °C)?
a) 5.0%
b) 0.5%
c) 100%
d) 0.72%
e) 7.2%
4. Calculate the concentrations and pH of all species present in a 1.0 M solution of H2CO3 (with Ka1 = 4.3 × 10-7 M; Ka2 = 5.6 × 10-11 M).
Salts and Acids and Bases
1. What is the pH of a salt solution containing 0.35 M of KBr?a) 0.46
b) 7.00
c) 13.54
d) 0.76
e) 13.24
2. What is the pH of a solution containing 0.35 M AlCl3? (Hint: Al3+ coordinates 6 water molecules to form Al(H2O)63+. One of the Al3+-coordinated waters has a Ka value of 1.4 × 10-5 M.)
a) 4.80
b) 7.00
c) 2.65
d) 4.15
e) 9.20
3. What is the concentration of OH- in a 0.10 M salt solution of NH4Br?
a) 4.8 × 10-8 M
b) 7.5 × 10-6 M
c) 1.0 × 10-13 M
d) 0.10 M
e) 1.3 × 10-9 M
4. What is the pH of a salt solution containing 0.2 M NaCN (the Ka of HCN is 4.9 × 10-10 M) ?
5. Calculate the Ka the cation and the Kb for the anion in a salt solution of NH4F.
Buffer Solutions and Titrations
1. What is the pH of a 0.1 L buffer solution containing 0.25 M CH3COOH and 0.5 M NaCH3COO?a) 4.43
b) 7.00
c) 5.04
d) 0.30
e) 2.37
2. What ratio of NH3 and NH4Cl would need to be mixed together to give a buffer solution with pH 9.5?
a) 0.55
b) 1.8
c) 1.0
d) 9.5
e) 0.020
3. How many moles of NaOH would be required to neutralize a 0.25 L solution of 0.62 M HBr?
a) 0.16
b) 0.32
c) 0.08
d) 1.2
e) 0.62
4. Imagine a titration of 100.00 mL of 0.02 M HF (Ka = 3.5 × 10-4 M) with 0.05 M NaOH. How many milliliters of 0.05 M NaOH are required to reach the equivalence point and what would the pH be?
a) 40 mL; 7.9
b) 20 mL; 7.0
c) 40 mL; 3.5
d) 40 mL; 7.8
e) 20 mL; 7.8
5. Suppose you wanted to make a buffer solution that would be resistant to the addition of small amounts of acid or base and hold a pH at 8.0. Which of the following compounds would be best to use?
a) CH3COOH; Ka = 1.8 × 10-5 M
b) C4H11NO3; Ka = 8.5 × 10-9 M
c) C8H17NO3S; Ka = 3.2 × 10-10 M
d) NH4+; Ka = 5.8 × 10-10 M
e) C4H4O4; Ka = 8.5 × 10-7 M
Properties that Determine Acid Strength
1. Which acid below is the strongest?a) H2O
b) H2Se
c) PH3
d) SiH4e) H2S
2. Which acid below is the weakest?
a) HClO3
b) HBrO3
c) HIO3
3. Which property of a molecule will have the greatest influence on its acid strength?
a) How big the overall molecule is
b) How hydrophobic the molecule is
c) How many oxygen atoms the molecule has
d) How strong the bond is between the proton that gets transferred and the other part of the molecule
e) How many hydrogen atoms the molecule has
4. Which acid is stronger?
a) CH3CH2OH
b) CH2FCH2OH
c) CF3CH2OH
d) CHF2CH2OH
5. What arrangement of compounds goes from the weakest to strongest acid?
a) H2SO3, HClO3, HClO4
b) HClO3, H2SO3, HClO4
c) HClO4, HClO3, H2SO3
d) HClO3, HClO4, H2SO3
e) H2SO3, HClO4, HClO3
Solutions
What Are Acids and Bases?
1. Which of the following bases satisfy the definition proposed by Brønsted and Lowry but do not satisfy the definition proposed by Arrhenius?I. Mg(OH)2
II. CH3CH2COO-
III. NaOH
IV. C5H5N
c) II and IV
Arrhenius's definition of a base was a bit shortsighted, but we'll cut him a break since it was 1844 and the Internet didn't exist yet. Without the help of Google, Arrhenius proposed that in order to be a base a substance has to release OH- to solution. Thus, molecules II and IV would not satisfy Arrhenius's definition because they do not have OH- in the first place to release to solution. Thankfully, Bronsted and Lowry came along to define bases like those of II and IV, which accept protons from water to generate OH-.
2. If the red boxes below represent an acid before dissociation into the blue boxes representing product concentrations, which of the three scenarios depicts the weakest acid?
Molecules do not look like red or blue bars. Repeat—molecules do not look like red or blue bars. Nevertheless, this problem is testing the concept of acid dissociation by using bars instead of proton acceptors and donors. The acid (red bar) that dissociates most fully into products (blue bars) is the strongest acid, which is depicted in choice III. Since no red bar is present after dissociation virtually all of the acid dissociated. The acid shown in I is an intermediate strength acid relative to the others.
Therefore, II is the weakest acid since most of the red bar remains after dissociation.
3. Label the conjugate acid-base pairs in the following chemical equation:
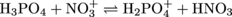
To identify conjugate acid-base pairs without drowning in the chemistry you'll first want to gain your bearings by finding the proton that is transferred. After careful comparison of the left and right sides of the equation you hopefully saw that NO3+ gained a proton and H3PO4 lost a proton. Because H3PO4 transferred a proton, it is the acid. The conjugate base of H3PO4 is the molecule that remains after the proton transfer, which is H2PO4-. Together, H3PO4 and H2PO4- make a conjugate acid-base pair. Similarly, NO3- accepts a proton so it is the base and the molecule that remains after the proton is accepted is the conjugate acid, HNO3. The two molecules make up the second conjugate acid-base pair.
4. Assuming equal concentrations of reactants and products, will the following acid-base reaction proceed to the right or to the left?
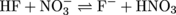
With acid-base reactivity, the good ol' days of the reaction simply going left to right are over. The direction of this reaction depends on which side the stronger acids and bases are on. Let's start with picking out the tougher acids. The two molecules that can transfer a proton are HF and HNO3. Who's stronger? If we were the betting type, we'd want to put our money on HNO3 as the stronger acid over HF.
Now let's look at the conjugate bases of those acids that can accept a proton, NO3- and F-. Put us down for F-beating as a base. So the stronger acid and the stronger base are on the right side of the equation. As with most struggles for power and glory, the desires of the stronger will prevail (unless you're the Roadrunner). In this case, the stronger acid HNO3 will fulfill its stronger desire to transfer a proton and the reaction will proceed right to left. Likewise, the stronger base F- will fulfill its stronger desire to accept a proton as the reaction goes from right to left.
5. The following reaction can be viewed as a Lewis acid-base reaction. Which molecule is acting as a Lewis acid and which is acting as a Lewis base?
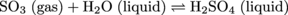
Remember that the Lewis definition focuses on what the lone-pair electrons are doing during the reaction. For the molecules above it helps to draw out the Lewis dot structure for each to identify lone pairs and see what happens to them during the reaction. In this reaction, lone pair electrons from water bond to the central sulfur atom to form the product H2SO4 (sulfuric acid). Therefore, water is the electron-pair donor, which qualifies it as a Lewis base. SO3 accepts the electron-pair, making it the Lewis Acid.
Just FYI, SO3 (sulfur trioxide) is the main ingredient in acid rain.
Water as an Acid and Base
1. If the concentration of H3O+ in a solution at 25 °C is 2.5 × 10-5 M, what is the concentration of OH-?e) 4 × 10-10 M
Every solution contains some proportion of H3O+ and OH- molecules; their concentrations will never be zero. The product of the H3O+ and OH- concentrations must equal Kw, which is 1 × 10-14 at 25 °C. To calculate [OH-], divide the Kw value by the [H3O+] given in the question.
2. The solution above is ______ .
c) acidic
The solution contains a H3O+ concentration greater than 1 × 10-7 M, and is therefore acidic.
3. At 60 °C the value of Kw increases from its value at 25 °C. The Kw value at 60 °C is 1.3 × 10-13. If the concentration of OH- in a solution at 60 °C is 3.6 × 10-7 M, what is the concentration of H3O+?
c) 3.6 × 10-7 M
No matter what the value of Kw is, the product of [H3O+] and [OH-] must equal Kw. As an aside, Kw gets larger as the temperature increases because the dissociation of water releases heat and therefore, by Le Chatelier's Principle, the equilibrium shifts to the products. To calculate [H3O+], divide the Kw value at 60 °C by the [OH-] given in the question.
4. The solution above is _______ .
a) neutral at 25 °C and neutral at 60 °C
At 60 °C the concentration of H3O+ is equal to the concentration of OH-, which makes the solution neutral at 60 °C. When the temperature is lowered to 25 °C, Kw will decrease to 1 × 10-14, but the relative populations of H3O+ and OH- will stay the same. Therefore, the solution will remain neutral at 25 °C as well.
5. What is the value for Kw if a neutral solution contains 1 × 10-6 M of H3O+?
d) 1 × 10-12
A neutral solution contains equal concentrations of H3O+ and OH- molecules. Therefore, if [H3O+] equals 1 × 10-6 M then [OH-] must also equal 1 × 10-6 M. The product of these values gives us Kw. In this case, Kw is larger than the value of 1 × 10-14 at 25 °C so the temperature of the solution in the question must be greater than 25 °C.
pH: Definition and Measurement
1. What is the pH of a solution at 25 °C that has an OH- concentration of 2.8 × 10-4 M?d) 10.45
There are two ways to arrive at the correct answer. The first way is to calculate the pOH by taking the negative log of the OH- concentration, which is 3.55. Subtracting from 14 gives the correct answer for the pH of 10.45. Alternatively, you could convert the OH- concentration to the H3O+ concentration by dividing Kw (1 × 10-14) by the OH- concentration given in the problem. Taking the negative log of the calculated H3O+ concentration gives us a pH of 10.45.
2. What is the pH of a solution at 100 °C that has a H3O+ concentration of 7.16 × 10-7 M?
a) 6.14
To find the pH from a given concentration of H3O+ take the negative log of the H3O+ concentration.
3. The solution in question 2 is _________. (Note that Kw at 100 °C is 51.3 × 10-14).
c) neutral
Recall the definitions for acidic, basic, and neutral: If [H3O+] > [OH-] the solution is acidic, if [H3O+] < [OH-] the solution is basic and if [H3O+] = [OH-] the solution is neutral. Given the Kw value at 100 °C you need to calculate the [OH-], which is 7.16 × 10-7 M. This concentration is the same as the H3O+ concentration! This means the solution is actually neutral. Most people think a neutral solution is always pH 7, but this is only true at 25 °C. The pH of a neutral solution will change depending on the temperature of the solution. Keep that in mind next time you're on Jeopardy! (or managing the pH of a public pool).
4. A solution has a pOH of 10.20 at 25 °C. What is the H3O+ concentration of this solution?
b) 1.6 × 10-4 M
This problem is the reverse of question 1. One way you could solve it is to first convert the pOH given in the problem to the pH by subtracting the pOH from 14. From this you'll find that the pH of this solution is 3.80. Convert the pH to H3O+ concentration using the equation [H3O+] = 10-pH. Alternatively, you could use the equation [OH-] = 10-pOH to calculate the OH- concentration. Then divide Kw at 25 °C to calculate the [H3O+]. Either approach will get you to the correct answer.
5. Pretend you want to measure the pH of a solution that you suspect is in the ballpark of pH 7.5. Which of the following acid-base indicators would you want to use? (Values in parentheses are the pH at which 50% of the indicator is in the protonated form and 50% is in the deprotonated form).
d) phenol red ( 7.7)
The human eye can typically detect changes in indicator color when the solution is within 1 pH unit of the pH at which the indicator is half protonated and half deprotonated. Phenol red is the only indicator whose color would be sensitive to pH changes around 7.5. At pH 7.5 the indicator would be yellowish-red. If the pH was greater than 8.7 the indicator would be pure red. If the pH was less than 6.7 the indicator solution would be pure yellow.
The Equilibria of Acids-Base Solutions
1. What is the pH of a 1.00 × 10-4 M solution of Ba(OH)2 solution (at 25 °C)?b) 10.3
The solution of Ba(OH)2 will dissociate entirely since it is a strong base. For every one molecule of Ba(OH)2 there will be 2 molecules of OH- produced. Therefore the concentration of OH- will be twice the concentration of Ba(OH)2 added. Taking the negative log of 2 × (1 × 10-4 M) gives a pOH value of 3.7. Subtracting this value from 14 give the pH value of 10.3.
2. If the red boxes below represented an acid before dissociation into the blue boxes representing product concentrations, list the acids in order of increasing Ka value.
The extent of dissociation indicates how strong an acid is. The stronger the acid, the larger the acid-dissociation constant (Ka) will be. The graphic above shows that acid III dissociates the most since no initial acid is visible after dissociation. This acid will have the largest Ka value. Acid I dissociates approximately 80% making it the next strongest acid. Acid II dissociates approximately 25% and is the weakest of the three acids and will have the lowest Ka value.
3. What is the percent dissociation of a 0.10 M solution of HNO2, which has a pKa value of 3.29 (at 25 °C)?
e) 7.2%
HNO2 is a weak acid. The concentration of HNO2 that dissociates can be calculated using the procedure that was used for CH3COOH in the section above. The pKa value of HNO2 can be converted to a Ka value using the relationship Ka = 10-pKa. The Ka value can be used to solve for the equilibrium concentrations of H3O+ and using the quadric equation or using algebra after making the simplifying assumption that the concentration of HNO2 remains constant. Solving the equation gives a concentration for H3O+ and of 0.0072 M. Because the HNO2 acid dissociation constant is much larger than the dissociation constant of water, approximately all of the H3O+ in solution will come from HNO2 dissociation. The percent dissociation can be calculated by dividing the concentration of HNO2 dissociated (0.0072) by the initial concentration of HNO2. Multiplying by 100% gives 7.2%.
4. Calculate the concentrations and pH of all species present in a 1.0 M solution of H2CO3 (with Ka1 = 4.3 × 10-7 M; Ka2 = 5.6 × 10-11 M).
H2CO3 is a polyprotic acid since it can transfer more than one proton. Because it can transfer exactly two protons it is more specifically called a diprotic acid. The extent of each proton transfer is indicated by the two (yes, two) acid-dissociation constants given in the problem.
Notice that the first dissociation constant (the transfer of a proton from H2CO3 to form HCO3-) is much larger than the second. (Incidentally, Ka values of polyprotic acids get smaller by several orders of magnitude for each additional proton release. This is because it's hard to keep removing a proton from a molecule that is already more negatively charged than it wants to be.) Therefore, the first proton transfer is the principle reaction and the second proton transfer, along with water dissociation, are the subsidiary reactions. Start by calculating the concentration of H3O+ and using Ka1 (x = [H3O+] = [HCO3-] = 6.6 × 10-4 M). Note that a simplifying approximation that the initial concentration of H2CO3 will not significantly change holds. Because this first proton transfer step is the principle reaction the concentrations of H3O+ and HCO3- will be the final equilibrium concentrations and their concentrations will not change significantly by the subsidiary reactions.
The concentration of CO32- can be calculated using the acid-dissociation constant for the second equilibrium (
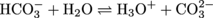). Because the second dissociation is a subsidiary reaction and will produce a negligible amount of H3O+ compared to the first dissociation, we can use the concentration of H3O+ produced from the first dissociation in the equilibrium relationship.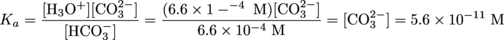 
Notice that the concentration of the second dissociation product, [CO32-], is equal to the second acid-dissociation constant. This will be true in general for weak diprotic acids.
It may seem like we're ready to hit the showers, but this problem isn't quite done. Water naturally dissociates into H3O+ and OH- on its own, so we should figure out the concentration of OH-, too. We can do that using the water-dissociation constant relationship:
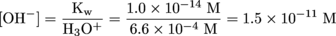
As usual, if you have a burning desire to know the pH of this solution, just take the negative log of the H3O+ concentration. You should get a pH value of 3.18. Okay, maybe that was a burning sensation instead of a burning desire. Time to hit the showers (to rinse this stuff off before it does too much damage).
Salts and Acids and Bases
1. What is the pH of a salt solution containing 0.35 M of KBr?b) 7.00
What do we have here? KBr salt? Don't worry. We haven't heard of it either. However, we only need to really figure out two things in order to solve this problem: 1) Does the cation (K+ in this case) or 2) the anion (Br- in this case) react with water? More specifically, we need to ask ourselves if K+ wants an OH- group, which would result in the production of H3O+ or if Br- wants a proton, which would result in the production of OH-. The answer to both is, NO. We know this because the Ka value of K+ is really tiny (its conjugate base, KOH, is really strong and its Ka is really big) and because the Kb value of Br- is also really tiny (its conjugate acid, HBr, is really strong. Therefore, the cation and anion will not react with water and the pH will not change. It will stay at 7.00.
2. What is the pH of a solution containing 0.35 M AlCl3? (Hint: Al3+ coordinates 6 water molecules to form Al(H2O)63+. One of the Al3+-coordinated waters has a Ka value of 1.4 × 10-5 M.)
c) 2.65
This problem is tricky because it contains a rather peculiar molecule, Al3+, which the hint tells us coordinates water molecules. We can just focus on dealing with Al(H2O)63+ because we know the Cl- ions released will not react with water (it's conjugate acid, HCl, is really strong). Notice that the Ka of Al(H2O)63+ is mush larger than the dissociation constant for water. Therefore, the Al(H2O)63+ acid equilibrium will be the primary reaction for calculating the equilibrium concentration of H3O+.
([H3O+] = √[(1.4 × 10-5) × 0.35M]; pH = -log([H3O+])
3. What is the concentration of OH- in a 0.10 M salt solution of NH4Br?
e) 1.3 × 10-9 M
First things, first: when the salt dissolves, releasing NH4+ and Br-, only NH4+ will react with water because Br- is a really weak base (it's conjugate acid is a strong acid, HBr). The dissociation of a proton from NH4+ is the principle reaction, which will determine the equilibrium concentration of H3O+ and OH-. Calculate the equilibrium concentration of H3O+ as usual using the method outlined in the guide (([H3O+] = √[(5.6 × 10-10) × 0.1M]. Then use the equilibrium concentration of H3O+ to calculate the equilibrium concentration of OH- using the relationship Kw = [H3O+][OH-] (Kw = 1 × 10-14).
4. What is the pH of a salt solution containing 0.2 M NaCN (the Ka of HCN is 4.9 × 10-10 M)?Is it us or are all these problems starting to seem the same? Once NaCN dissolves, Na+ will just chill, but CN- will react with water (it's conjugate acid is weak). CN- will act as a base so first convert the Ka of its conjugate acid to a Kb using the relationship Kw = Ka × Kb. Now using the Kb value calculate the equilibrium concentration of OH- (([OH-] = √[(2.0 × 10-5) × 0.2M]. The pOH equal –log([OH-]). Convert the pOH to pH using the relationship pH = 14 – pOH. The pH is 11.30.
5. Calculate the Ka the cation and the Kb for the anion in a salt solution of NH4F.
When the salt solution dissolves, NH4+ will be the cation and F- will be the anion. NH4+ will act as an acid and its Ka value can be calculated from the Kb value of its conjugate base, NH3 (Kb = 1.8 × 10-5 M) using the relationship Kw = Ka × Kb (did we mention this was an important relationship?). F- will act as a base and its Kb value can be calculated from the Ka value of its conjugate acid, HF (Ka = 3.5 × 10-4 M) using the same relationship, Kw = Ka × Kb.
Buffer Solutions and Titrations
1. What is the pH of a 0.1 L buffer solution containing 0.25 M CH3COOH and 0.5 M NaCH3COO?c) 5.04
The Henderson-Hasselbalch is the go-to equation for this one. The [HA] in this case is 0.25 M and the [A-] concentration is given by the concentration of NaCH3COO, which fully dissociates leaving 0.5 M CH3COO-. The pKa for the weak acid is 4.74 and log(4.74) equals 0.30. The sum of these is 5.04.
2. What ratio of NH3 and NH4Cl would need to be mixed together to give a buffer solution with pH 9.5?
b) 1.8
Henderson-Hasselbalch reprise. This time, substitute the pKa of the acid, NH4+ (9.24) and the desired pH (9.5) to solve. A little algebra gives a value of 1.8.
3. How many moles of NaOH would be required to neutralize a 0.25 L solution of 0.62 M HBr?
a) 0.16
The 0.25 L solution of 0.62 M HBr contains 0.16 moles of H+ (moles = molarity/volume) since HBr is a strong acid and is fully dissociated in solution. To neutralize the solution 0.16 moles of OH- must be added. Because for every one molecule of NaOH there is one molecule of OH-, 0.16 moles of NaOH must be added to neutralize the solution.
4. Imagine a titration of 100.00 mL of 0.02 M HF (Ka = 3.5 × 10-4 M) with 0.05 M NaOH. How many milliliters of 0.05 M NaOH are required to reach the equivalence point and what would the pH be?
d) 40 mL; 7.8
At the equivalence point, the concentration of OH- added equals the amount of HF that would be initially present. A 100.00 mL solution of 0.02 M HF contains 0.002 moles of HF initially. To get to the solution's equivalence point 0.002 moles of OH- must be added. Getting 0.002 moles of OH- from a 0.05 M NaOH stock solution would require adding 40 mLs [M = (moles)/(Liters); 0.05 M = (0.002 moles)/(0.04 L)]. The addition of this 40 mLs of NaOH brings the solution volume to 140 mLs. To calculate the pH of this solution recall that the principle reaction at the equivalence point is the reaction of the conjugate base, F- in this case, with water:
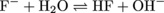
The equilibrium constant for this reaction (Kb) can be solved using the Ka value given in the problem and the relationship Ka × Kb = Kw [(3.5 × 10-4)(Kb) = (1 × 10-14)]. Using the initial concentration of the species and the Kb value (2.9 × 10-11) allows the concentration of OH- to be computed using the method detailed in section 4. The initial concentration of F- is computed using the total reaction volume (140 mL) and the moles of F-, which at the equivalence point equals the initial moles of HF (0.002). yielding an initial F- concentration of 0.014 M. Only a small fraction of this is converted to OH- since Kb is so small so the assumption that the initial concentration of F- stays essentially constant is valid. Therefore, the final equation to solve for the concentration of OH- is:
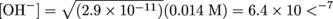
The pOH = -log([OH-]) and pH = 14 – pOH leading to a pH value at the equivalence point of 7.8.
5. Suppose you wanted to make a buffer solution that would be resistant to the addition of small amounts of acid or base and hold a pH at 8.0. Which of the following compounds would be best to use?
b) C4H11NO3; Ka = 8.5 × 10-9 M
The buffering capacity of a buffer is greatest when the solution pH is equal to the pKa of the weak acid buffer. To answer this question, convert the Ka values of each compound given using the equation, pKa = -log(Ka). The compound in (b) has a pKa value of 8.07, which is the pKa value closest to pH 8 of all the compounds listed. Incidentally, C4H11NO3 (2-Amino-2-hydroxymethyl-propane-1,3-diol) is a common buffer used in biochemical research to hold solutions near physiological pH values.
Properties that Determine Acid Strength
1. Which acid below is the strongest?b) H2Se
The two trends to think about for this problem are atom size, which increases down a group in the Periodic Table and bond polarity, which increases across a row in the Periodic Table. The molecule with the largest central atom and most polar bonds will be the strongest acid. H2Se is stronger than H2O and H2S because Se is larger than both O or S. H2Se is also stronger than either PH3 or SiH4 because the Se-H bond is more polar than both the P-H bonds and Si-H bonds.
2. Which acid below is the weakest?
a) HClO3
The only difference between each acid is the size of the central atom. As the size of the central atom increases, the H-O bond gets weaker. Therefore, the acid with the largest atom, Iodine, will be the strongest acid and the acid with the smallest will be the weakest.
3. Which property of a molecule will have the greatest influence on its acid strength?
d) How strong the bond is between the proton that gets transferred and the other part of the molecule
The bond between the proton that gets transferred and the rest of the molecule must break in order for the molecule to act as an acid. Therefore, its strength will ultimately determine the strength of the acid. In this section we talked about two factors, the size of the atom that is bonding to the transferable proton and the polarity of the bond that must break, that influence the strength of the bond. The other properties listed do not significantly influence the acid strength relative to these other more important factors.
4. Which acid is stronger?
c) CF3CH2OH
Fluorine, like oxygen, is very electronegative so it likes having excess pairs of electrons around. So, the more fluorine atoms are attached to the molecule the stronger the acid will be because dissociation of the proton results in an addition electron pair. Even though the fluorine atoms are several bonds away from the oxygen atom that gets the lone pair, their attraction for electrons can be long-distance. This deep electron love by the fluorine atoms stabilizes the product of the acid dissociation reaction (the conjugate base), making the molecule a stronger acid.
5. What arrangement of compounds goes from the weakest to strongest acid?
a) H2SO3, HClO3, HClO4
For this problem both the number of oxygen atoms attached to the central atom of the molecule and the identity of the central atoms is changing. For H2SO3 and HClO3 only the central atom is different but both atoms fall in the same row on the Periodic Table. Because electronegativity increases going across a row from left to right, the Cl containing molecule will be more acidic. Because HClO4 has more oxygen atoms attached to the central atom (more electron vacuum cleaners) it will be stronger than HClO3 (and even stronger than H2SO3).