Think you’ve got your head wrapped around Congruent Triangles? Put your knowledge to
the test. Good luck — the Stickman is counting on you!
Q. It is stated that ∆BAC ≅ ∆EAD. What makes this statement true? 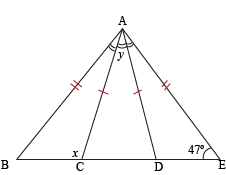

SSS
SAS
ASA
AAS
The statement is false; ∆BAC ≇ ∆EAD
Q. Is ∆ABD ≅ ∆CBD?

Yes, by SSS
Yes, by SAS
Yes, by ASA
Yes, by AAS
No
Q. Which of the following statements are true about ∠ABD and ∠CBD?

They are supplementary.
They are congruent.
They are right.
(A) and (B)
All of the above.
Q. Why is ΔABD congruent to ΔACD?

SSS
Actually, they're not congruent.
ASA
AAS
SSA
Q. How can we tell that ∠BAD is congruent to ∠ADB?

ΔABD is isosceles.
SSA
Because they're supplementary.
SAA
We can't.
Q. Since ∠BAD ≅ ∠ADB, and m∠BAD + m∠ADB = 90, this means that:

m∠ADB = 45
m∠BAD = 45
m∠CAD = 45
m∠CDA = 45
All of the above
Q. Which is true about AD?

It bisects ∠CAB
It bisects ∠CDB
It is congruent to AB, BD, DC and AC
Both (A) and (B)
All of the above
Q. When is SSA enough information to conclusively prove that two triangles are congruent?
Always
Only when the angle in question is less than 90°
Only when another angle has been determined to be 90°
Only when the angle in question is greater than 90°
Never
Q. Is ∆ABC congruent to ∆EDC?

Yes, by SSS
Yes, by SAS
Yes, by ASA
Yes, by AAS
No
Q. Which piece of given information would be enough to prove that ΔABC was congruent to ΔEDC?

AB ≅ AD
∠ABC is a right angle
∠ADC ≅ ∠CED
Both (A) and (C)
None of the above