The equation of an ellipse is  . . The center is at (h, k), which is (-3, 3) in this case. It's easy to see that a = 10, but where did b go? It's still there, underneath y, we just can't see it because it is 1. Very sneaky, b. We can already find all four vertices for the ellipse. a is the horizontal distance from the center to two of the vertices, and b is the vertical distance for the other two. x and a go together, and so do y and b. This gives us: (-3 ± 10, 3) and (-3, 3 ± 1) (-13, 3), (7, 3), (-3, 2), and (-3, 4) The ellipse axis parallel with the x-axis is definitely bigger than the one parallel to the y-axis. That makes a = 10 the length of the semi-major axis, and the ellipse as a whole is horizontal. That's all we need to know to find f, the distance to the foci. We're on to you, f, and your accomplice, f2. To find him, we take the square of the semi-major axis and subtract away the square of the semi-minor axis. f2 = a2 – b2 = 100 – 1 = 99 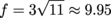
The foci fall on the major axis, so we'll add and subtract f from the x-coordinate of the center. (-3 ± 9.95, 3) (-12.95, 3) and (6.95, 3) Oh boy, now we've done it. Actually, we've solved the problem. That's the thing we did. Nothing wrong with that. | |