Two lines walk into a bar. They order the same drinks, dance the same dances, but end up leaving without having ever met. That's the story of parallel lines.

Parallel lines will never intersect. This is because they share the same slope. If one line rises by 1, so does the other. A run of -3 is perfectly matched. We could watch this all day.
Sample Problem
Show that the lines passing through these points are parallel.
(0, 5) and (2, -1)
(-1, 5) and (1, -1)
Parallel lines have never met before now, and will never meet in the future. How can we possibly predict the future of these two lines? Our crystal ball is busted, so we'll resort to showing that they have the same slope, instead.
The formula for the slope is:

We'll just plug in the points from the first line into the equation. It doesn't matter which one we call point 1 and which one is point 2, as long as we stay consistent. It's like the old saying goes: you can pick your points, and you can pick your friends, but you can't pick your friends' points.

Now we can find the slope of the second line. Let's do (-1, 5) for the second point, the one being subtracted.

Two lines with the same slope? That's parallel lines in a nutshell. Except we don't think that they'd fit in a nutshell. They'd have to meet at some point in there, right?
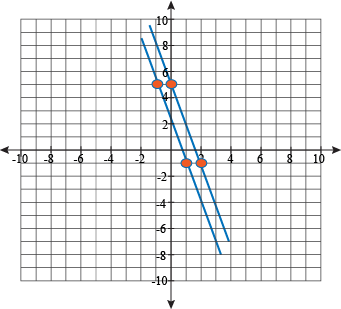
The graph of the two lines shows the same thing. They share a slope, they never meet, and they are definitely not inside a nutshell.
A different relationship between two lines is when they intersect so hard that they can't intersect any harder.

These are perpendicular lines. They meet at a 90-degree angle to each other. Even so, they are total opposites of each other. Like, partners in a buddy cop movie kinds of opposites.

Perpendicular lines have slopes that are the negative reciprocals of each other. Like this:

It's not just the negative slope, but the negative upside-down slope.
Sample Problem
Show that the lines passing through these points are perpendicular.
(-1, 7) and (1, -5)
(-6, 0) and (12, 3)
Once again, the key to solving this problem is to find the slopes of both lines. It's a good thing we're so pro at this.

Plugging in points from the first line:

One slope down, one more to go. Or should we say, one slope down and one up.

Yep, -6 and  are negative reciprocals. We can double-check this by multiplying them together: their product should equal -1, and it does.
are negative reciprocals. We can double-check this by multiplying them together: their product should equal -1, and it does.

We can double-check our double-check by graphing as well. The graph agrees with us, too. We love it when a plan comes together.