f has a vertical asymptote at x = 0, and no holes. We can start drawing: 
Since the degree of the numerator and denominator are the same, f has a horizontal asymptote at y = 3: 
f is 0 when its numerator is 0 and its denominator is not. This occurs when  . . The only thing left is to find where f is negative and positive. When  the numerator and denominator are both negative, therefore f is positive. When the numerator and denominator are both negative, therefore f is positive. When  , the numerator is positive and the denominator is negative, so f is negative. , the numerator is positive and the denominator is negative, so f is negative. 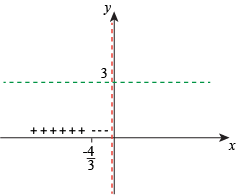
We now have enough information to get a rough sketch of the piece of f that lies to the left of the vertical asymptote at y = 0. 
When x > 0, the numerator and denominator are both positive and f is positive. Since f must approach its asymptotes, f looks like this: 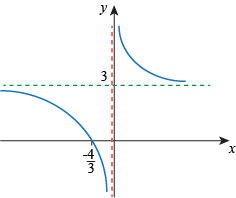
We didn't need to worry about f(0) for this function, since f is undefined at 0. A number line is a useful tool for figuring out where a function is negative and positive, and we'll use this tool in one of the examples. Wherever f is 0 or undefined, its sign has the ability to change. Draw a number line and mark all the values of x where f is 0 or undefined. From this, find the sign of f in between those marked values. |