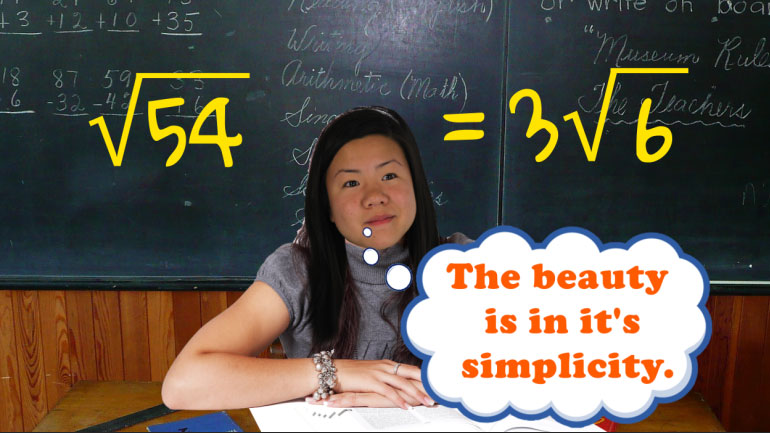ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
Playlist ACT® Elementary Algebra 26 videos
ACT Math: Elementary Algebra Drill 1, Problem 1. What is Ben's current age?
ACT Math: Elementary Algebra Drill 1, Problem 2. Can you simplify the expression?
ACT Math Elementary Algebra: Drill 1, Problem 3. Solve for y using substitution.
ACT Math 5.5 Elementary Algebra 327 Views
Share It!
Description:
ACT Math: Elementary Algebra Drill 5, Problem 5. How much 10% solution must be added to yield the correct concentration?
- Elementary Algebra / Linear equations
- Product Type / ACT Math
- Foreign Language / Arabic Subtitled
- Foreign Language / Korean Subtitled
- Foreign Language / Chinese Subtitled
- Foreign Language / Spanish Subtitled
- Mathematics and Statistics Assessment / Word Problems and Applications
- Pre-Algebra / Data collection, representation, and interpretation
Transcript
- 00:03
Time to get your shmoop on...
- 00:05
Monty has 2.5 liters of a 4% solution and
- 00:08
one container of 10% solution. How much 10% solution does he need to add
- 00:14
to the 2.5 liters of the 4% solution to get a 6% solution?
- 00:19
And here are the potential answers...
Full Transcript
- 00:26
Okay, It's all about concentration levels... like in a sports drink, really.
- 00:30
Like... ever cut a bottle of Gatorade with water? Same idea.
- 00:34
Let's say we just finished a brutal 2 on 1 against Kobe and Lebron and sweated 2.5 liters.
- 00:40
The "watered down" Gatorade has 4% sugar; and the normal Gatorade has 10% sugar.
- 00:46
We're sorta like the 3 bears in this sense -- we want the porridge neither too hot nor
- 00:50
too cold...
- 00:51
...the Gatorade has to be somewhere in between the 4 and the 10, and we think 6% is about
- 00:57
the right concentration to replace the electrolytes we lost dragging Kobe and Lebron up and down the court.
- 01:02
To help frame even further
- 01:03
Now let's do the math. We can write 2.5 liters of 4% solution as
- 01:10
2.5 times .04, which is 0.1.
- 01:12
Monty has x liters of 10% solution, so x times .1 is .1x.
- 01:17
Together, the 6% solution will have 2.5 liters plus x, which we can write as .06 times the
- 01:26
quantity 2.5 plus x.
- 01:28
Distributing the .06...we have .15 plus .06x. So if we set up the equation... 0.1 plus 0.1x
- 01:37
equals .15 plus .06x. Combining like terms...which means grouping
- 01:42
the x's together and the constants together, we get that .04x equals .05.
- 01:49
Divide both sides by .04, and x equals 1.25, or 1 and 1/4 liters...
- 01:55
Looks like B is our answer.
Related Videos
ACT Math: Plane Geometry Drill 3, Problem 1. What is the area of the trapezoid shape in the video?
ACT Math: Coordinate Geometry Drill 1, Problem 1. Which inequality is expressed by the number line?
ACT Math: Intermediate Algebra: Drill 3, Problem 1. Find the fifth number in the series.
We don't like knocking people down to size, but we do like simplifying radicals. Join us?
If fleeing criminals always fled the scene of the crime at perfect right angles, it would be much easier to determine their whereabouts. Fortunatel...