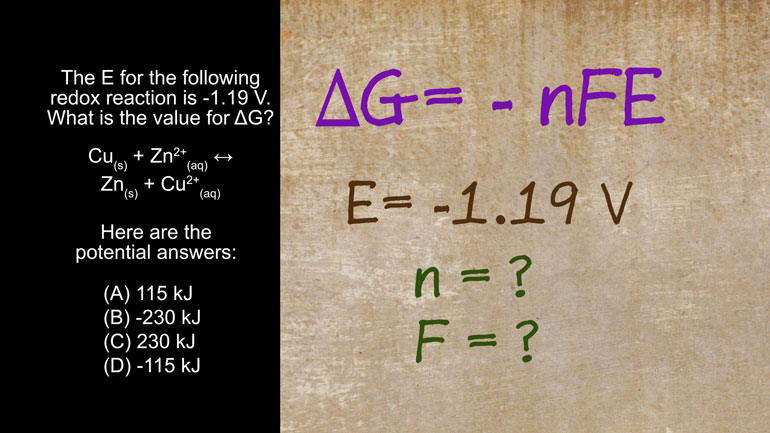ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
AP Chemistry Videos 45 videos
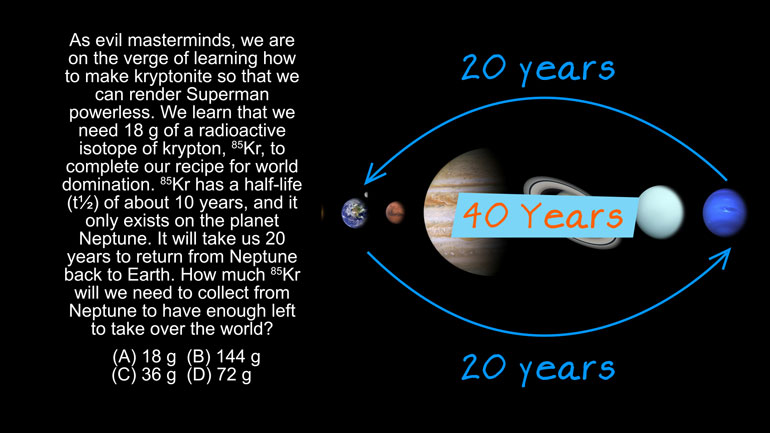
AP Chemistry 3.5 Chemical Reaction Rates. How much 85Kr will we need to collect?
Want to pull an Oliver Twist and ask us for more? We've gotcha covered. Head over to /video/subjects/test-prep/ap/ap-chemistry/ for more AP Ch...
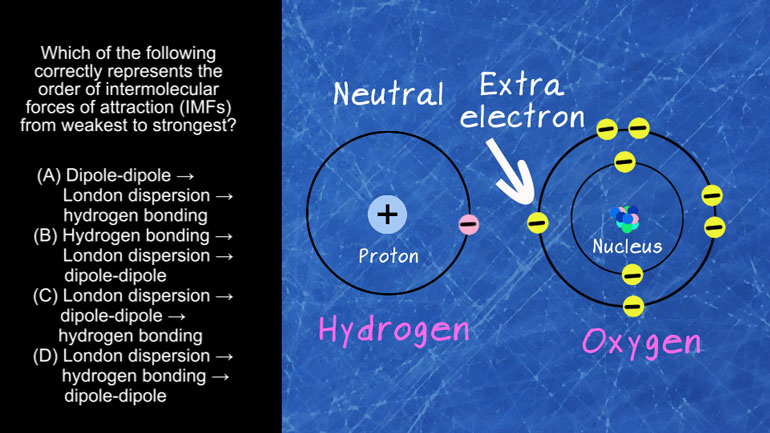
AP Chemistry 1.3 Forming and Breaking Bonds. Which of the following ions are spectator ions?
AP Chemistry DBQ/Free Response 251 Views
Share It!
Description:
AP Chemistry DBQ/Free Response. Perform the following calculations.
Transcript
- 00:04
Here's your shmoop du jour, brought to you by balloons. Aside from being kicked in a
- 00:08
sensitive area, they're still the number one way to talk in a high-pitched voice.
- 00:15
A party is thrown with balloons. The balloon salesman tells the party planners that he
- 00:19
is out of helium cylinders, but he has a stock of other gases: hydrogen, argon, and chlorine.
- 00:26
The party planners see an unlabeled gas cylinder in the back of the store. They are curious
Full Transcript
- 00:30
as to which gas it is. They fill a balloon to 1 liter and weigh it.
- 00:35
NOTE: We do NOT recommend filling balloons with random, unlabeled gas. These guys are
- 00:40
professional idiots...do not try this at home... Anyway, after subtracting the weight of the
- 00:45
balloon, they find that the weight of the gas in the balloon is 0.819 grams
- 00:50
It is 27 degrees Celsius outside with standard atmospheric pressure. Assume ideal behavior
- 00:57
for all gases. Air has a density of 1.161 grams per Liter under these conditions.
- 01:03
So for Part A, we need to perform the following calculations:
- 01:07
1 - Calculate the density in grams per Liter of hydrogen.
- 01:11
2 - Calculate the density in grams per Liter of argon.
- 01:14
3 - Calculate the density in grams per Liter of chlorine.
- 01:21
First things first: Calculate the density in grams per liter of hydrogen.
- 01:25
Okay, so this problem mentions that we're working with gases, and that we can assume
- 01:29
ideal behavior for all gases. So...we can assume that none of them is going
- 01:33
to be resting their elbows on the dinner table. We should automatically be thinking about
- 01:38
the ideal gas law... PV equals nRT. This law allows us to find certain properties
- 01:44
about an ideal gas...where p equals pressure, v equals volume in liters, n equals number
- 01:50
of moles, R is the ideal gas constant, and T is temperature in Kelvin.
- 01:58
What's an ideal gas, you might ask? It's a hypothetical gas in which atoms are perfectly
- 02:03
elastic and there are no intermolecular attractive forces between molecules. They're all...VERY
- 02:09
attracted to each other. But back to solving the problem.
- 02:14
Ok, so we're given standard atmospheric pressure, which means that P equals 1 atmosphere, the
- 02:20
gas constant R equals .0821, and the temperature equals 27 degrees Celsius.
- 02:27
But we have to convert temperature to Kelvin...
- 02:29
and to do so, we can add 273 to 27...to get 300 Kelvin.
- 02:35
Plugging all these numbers into the equation,
- 02:37
we find that V equals n times .0821 times 300. But that doesn't look anything like density,
- 02:44
which is in units: grams per liter. So what else do we know about hydrogen gas
- 02:49
that can help us? It's molecular weight -- bingo.
- 02:53
We can calculate the molecular weight of hydrogen gas, which is 2 times the weight of two hydrogen
- 02:58
atoms, using the periodic table. This equals 2.106 grams per mole.
- 03:04
Using dimensional analysis, to convert grams per mole into grams per liter, we know that
- 03:08
we have to have moles on the top, and liters on the bottom, which is equivalent to n over V.
- 03:16
Now we know what to do with our ideal gas
- 03:18
law equation. N over V equals 1 over .0821 times 300, or .0406 moles per Liter.
- 03:30
Multiplying this by the molecular weight of hydrogen gas, we can convert our value into density.
- 03:36
So we have .0406 moles per liter times 2.106 grams per
- 03:40
mole equals .0855 grams per liter. But we can't forget about significant figures
- 03:47
either! All the numbers we're given in the problem have three sig figs, so our answer
- 03:52
should have three as well. So great.
- 03:56
Now we just need to do the same thing
- 03:57
for the other 2 calculations... Let's find ourselves the density of argon.
- 04:02
Because we are assuming ideal gas behavior, this calculation will be the same as the calculation
- 04:06
in part 1 to obtain the value for n over v... ... .0406 moles per liter.
- 04:12
For ideal gases, this value is independent of the identity of the gas.
- 04:16
We use the molecular weight of argon -- 39.948 grams per mole...which we can find from the
- 04:22
periodic table again....to convert this value to density.
- 04:26
0.0406 moles per liter times 39.948 grams per mole equal 1.62 grams per liter.
- 04:35
Okay, and now for the density of chlorine. Same deal, but this time we use the molecular
- 04:39
weight of chlorine - 70.905 grams per mole. We can multiply .0406 times 70.905 to get
- 04:47
2.88 grams per liter.
- 04:52
OK...Now for part B of this question...
- 04:55
Assuming the party planners want their balloons to float, which of the three listed gases
- 04:59
should they purchase? Justify your answer.
- 05:04
Well, if we ever want something to float in
- 05:06
another, we need the thing we want to float to have a LOWER density than the other.
- 05:14
Since air has a density of 1.161 grams per Liter, as given in the problem...we want the
- 05:19
gas that has a density less than that....
- 05:21
Hydrogen has a density of 0.0855 grams per Liter, so that's our answer!
- 05:31
Time for Part C...
- 05:33
Let's take question 1 first... what is the molecular weight and the identity of the gas
- 05:37
in the unlabeled cylinder, assuming it is monatomic and acts as an ideal gas?
- 05:44
Ok...so this question is asking us to figure out the molecular weight and identity of the
- 05:48
unknown gas. We're given that the weight of the gas in the balloon is 0.819 grams.
- 05:53
But molecular weight is in the unit: grams per mole...so all we have to do is figure
- 05:57
out the number of moles, using the ideal gas law again, PV equals nRT.
- 06:03
Rearranging the equation to find moles, n equals PV divided by RT.
- 06:10
We have all the information we need to solve: standard pressure -- P equals 1 atmosphere...
- 06:16
volume -- V equals 1 Liter, gas constant -- (R = 0.0821 liters atmospheres over moles times
- 06:24
Kelvin), and temperature -- T equals 300 Kelvin.
- 06:28
We plug in the numbers and solve for n:
- 06:30
1 times 1 over .0821 times 300 equals .0406 moles.
- 06:38
So the molecular weight is grams per mole.... .819 grams divided by .0406 moles equals 20.2
- 06:44
grams per mole. Looking at the periodic table, the element
- 06:47
with that molecular weight is Neon.
- 06:51
Now the question wants to know...will it float?
- 06:54
Well, like part B of this question, the key to figuring out if a gas will float is if
- 06:59
it is less than the density of air. The density of neon is in grams per liter...so
- 07:06
.819 grams divided by 1 liter is .819 grams per liter.
- 07:11
0.819 grams per liter is less than 1.161 grams per liter...so yeah, it totally floats!
- 07:20
Finally... Part D... Question 1 of part D... Write the balanced,
- 07:25
net ionic equation for the reaction that occurs when chlorine gas is bubbled into a solution
- 07:30
of sodium bromide. Alright, to be honest, we know this question
- 07:33
is kinda unrelated to the rest of the problem. But sometimes the test makers are like that,
- 07:37
and we just have to... deal with it. So to find the net ionic equation, we first have to start
- 07:41
with the balanced molecular equation. Chlorine gas into sodium bromide...chlorine
- 07:46
gas is a diatomic molecule, so we have Cl2. The formula for sodium bromide is NaBr.
- 07:55
This is an example of a single displacement chemical equation...so the chlorine replaces
- 07:59
the bromide to make sodium chloride gas and bromine gas...which is a diatomic molecule.
- 08:06
So we have two bromine atoms, not just one. To balance this equation, we can add a 2 in
- 08:11
front of the sodium bromide and 2 in front of the NaCl.
- 08:16
To find the net ionic equation, we have to break all the soluble electrolytes into their
- 08:21
ions... ...which means the sodium ions on both sides
- 08:24
need to be taken out of their salts.
- 08:28
Just like a normal math equation, we can cancel
- 08:30
out the two sodium ions on the left and right...and we're left with chlorine gas plus 2 bromide
- 08:35
ions, which makes bromine gas and 2 chlorine ions.
- 08:40
Number 2 in part D. Last question...asks us which species is oxidized in the equation.
- 08:48
Well, oxidation occurs when an element becomes positive because they are LOSING electrons.
- 08:53
Good for them. We don't become positive when we lose ANYTHING.
- 08:58
If we look at our net ionic equation, the bromide ions are being oxidized because, on
- 09:02
the left, they have a negative charge, but then after the ions react with the chlorine
- 09:06
gas, they have no charge. They are becoming more positive, or being oxidized!
- 09:11
Phew. So thanks for hanging in there with us for that one. It was a beast.
- 09:15
Hello? Oh...don't tell us we have to say all that all over again...
Related Videos
AP Chemistry 1.3 Chemical Reaction Rates. What is the overall order of the reaction?
AP Chemistry 1.4 Chemical Reaction Rates. What are the correct units for a second order rate constant?
AP Chemistry 1.5 Chemical Reaction Rates. What is the rate law for the reaction?
AP Chemistry 3.2 Laws of Thermodynamics. What is the value for ΔG?