ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
Geometry Videos 51 videos
If you were looking for the trailer for the new Michael Bay movie, you've got the wrong number. Transformations are rotations, reflections, and tra...
Translations: now without the trans fat. Functions: now without the…fun? Wait, scratch that. Now with extra fun! Don’t believe us? There's only...
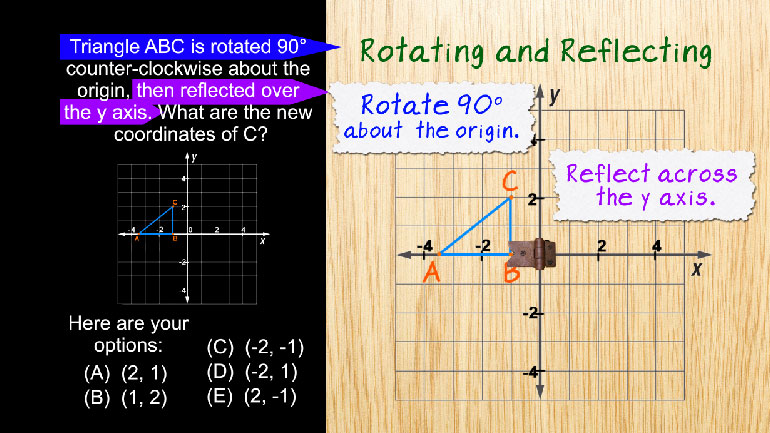
Measurement and Geometry Drill 5 Problem 4. Which of the following best describes the transformation as shown in the graph below?
SAS, ASA, AAS 2625 Views
Share It!
Description:
This video is sort of a PSA for SAS, ASA, and AAS. This stuff might show up on the ACT, so watch it ASAP.
Transcript
- 00:03
SAS, ASA and AAS, a la Shmoop.
- 00:07
Henry has always been a proficient wizard,
- 00:10
but lately, it seems all of his potions have been turning out… a little funky.
- 00:14
Henry is setting out to solve the problem logically.
- 00:18
First, he double-checks his ingredients. They all seem to be in order.
Full Transcript
- 00:21
Next, his spell book. Looks fine. Finally, his two hourglasses.
- 00:25
If the two halves of the hourglasses are differently shaped, or incongruent, the timing will be all off.
- 00:32
Henry may have found the problem.
- 00:34
Now the fastest way for Henry to determine congruency
- 00:37
would be just to measure all the sides and angles.
- 00:40
Unfortunately, Henry lost his measuring tools…
- 00:43
…and he only has a few measurements originally provided by the hourglass manufacturers to work with…
- 00:47
…as well as three very useful geometric rules.
- 00:50
Each hourglass can be divided into two triangles, one standing upside down on the other.
- 00:55
One rule for determining congruency between triangles is the Side-Angle-Side Rule, or
- 01:00
SAS, which states…
- 01:03
…“If two sides and the angle between them of one triangle are congruent to the
- 01:07
corresponding parts of another triangle, the triangles are congruent.”
- 01:11
For the smaller hourglass, Henry has the measurements of two of the sides;
- 01:16
5 inches and 8 inches, and 5 inches and 8 inches.
- 01:20
The measurements are equal, so the sides are congruent; we can use hash marks to keep track
- 01:26
of congruent parts.
- 01:28
As for the angle between them, Henry can use the Vertical Angle Theorem to conclude that
- 01:33
the angles are also congruent.
- 01:35
So by the SAS rule, the two triangular halves of this hourglass are congruent.
- 01:41
Another rule for determining triangular congruency is the Angle-Side-Angle Rule,
- 01:45
or ASA, which states…
- 01:47
…“If two angles and the side between them of one triangle are congruent to the
- 01:51
corresponding parts of another triangle, the triangles are congruent.”
- 01:55
The triangles of Henry’s second hourglass have congruent corresponding angle measurements…
- 01:59
…but that doesn’t prove congruency because the two halves might still be different sizes.
- 02:04
So Henry measures the bases; and there you go they’re congruent!
- 02:09
Since the bases lie between congruent, corresponding angles, the two halves of this hourglass are
- 02:14
congruent by the ASA rule.
- 02:17
Related to the ASA rule is the Angle-Angle-Side Theorem, or AAS, which states…
- 02:24
…“If two angles and an adjacent side of one triangle are congruent to the corresponding
- 02:30
parts of another triangle, the triangles are congruent.”
- 02:34
This theorem is a bit of a shortcut because it helps save a few steps in any proof…
- 02:38
…namely, if you know two angle measurements of any triangle, you can easily find the third.
- 02:43
Looks like there isn’t really anything wrong with the shape of Henry’s hourglasses.
- 02:48
Back to the drawing board.
Related Videos
This video covers the different types of triangle. What makes a triangle isosceles, scalene, or equilateral? What about the different kinds of angl...
Sine is the opposite over the hypotenuse; cosine is the adjacent over the hypotenuse; and tangent is the opposite side over the adjacent side....
Someday you might be a big, fancy defense lawyer, and you'll have to prove that your client's triangle was congruent to the triangle in question. W...
You might not think that the properties of a triangle would be particularly helpful in the realm of Tootsie Pop lickology. But boy, would you be wr...
How does learning about triangle angles and types of triangles while being told a story about Goldilocks sound to you? Not too shabby. Grab a snack...