ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
Ratios, Percentages, and Proportions Videos 55 videos
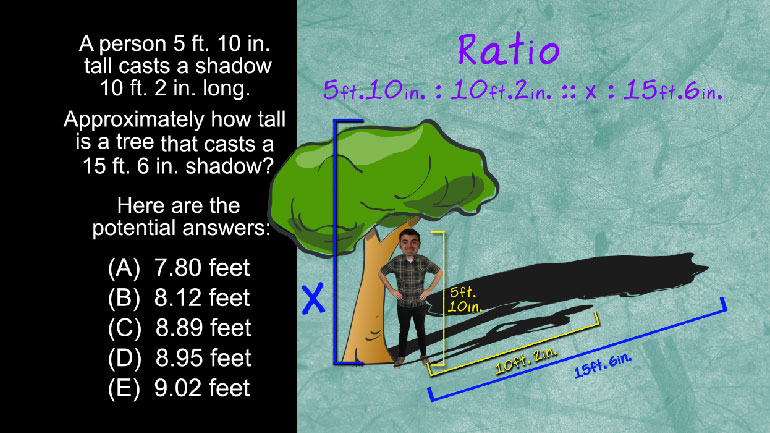
SAT Math 10.3 Geometry and Measurement. What is the ratio of birds to dogs?
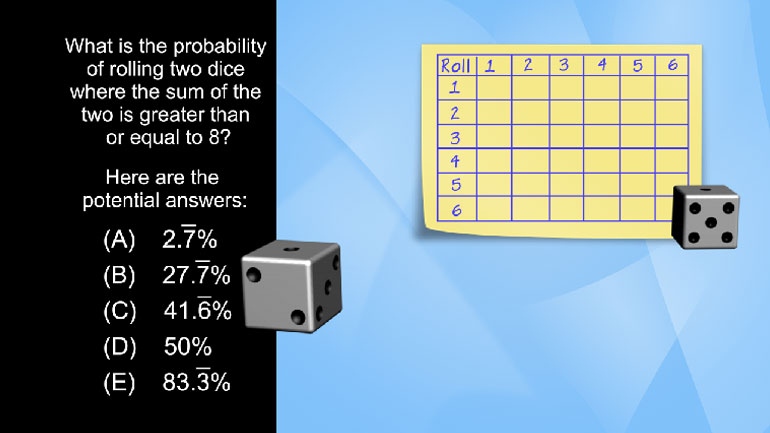
SAT Math 2.1 Statistics and Probability. Which two items have the highest protein to fat ratio?
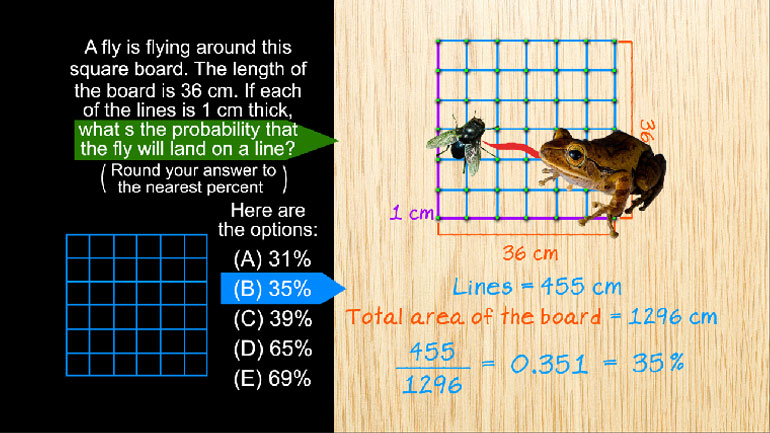
SAT Math 2.2 Statistics and Probability. What percent of her recommended daily intake of 2000 calories did she consume?
Word Problems with Percents 659 Views
Share It!
Description:
If the value of a painting increases by 15 percent every year, what was it worth 5 years ago? Hold up: why would you want to sell it now? In a few more years, you could be a millionaire. Patience is key.
Transcript
- 00:00
Percents, a la Shmoop. Have you ever wanted a system you can use
- 00:00
to judge just about anybody’s performance? You’ve probably heard percents mentioned
- 00:00
during sporting events. Or seen them on your graded tests.
- 00:00
Just about any statistic can be expressed with a percentage.
- 00:00
Although some things really shouldn’t be expressed that way…
Full Transcript
- 00:00
When you express something as a percent, you are really determining how much per every
- 00:00
100. The same way cents are a portion of a dollar,
- 00:00
percents are a portion of 100%. Suppose you answered 24 out of 25 questions
- 00:01
correctly on your test. You just like to wreck the curve for everybody,
- 00:01
don’t you? First we find out how many times 25 goes into
- 00:01
100. So we can multiply 25 by 4 to get our magical number of 100. Then we multiply 24
- 00:02
by 4, which equals 96. Congratulations! You got a 96% on your test.
- 00:02
Percents pop up just about anywhere you can imagine.
- 00:02
For example, money matters are often expressed using percents.
- 00:03
Here’s a hint: the percentages in credit card terms and conditions usually are not
- 00:03
on your side – the best APR’s come in small packages.
- 00:03
Even seemingly small percentage changes in the stock market can have massive real-world
- 00:04
effects. Percents are a key part of the language of
- 00:04
economics, and sometimes just thinking in percents helps people to make good financial
- 00:04
decisions. For example, even if an outfit is “totally
- 00:04
super cute” you probably shouldn’t buy it if it costs more than fifty percent of
- 00:06
your net worth. If you’re a sports fan, you’re used to
- 00:06
hearing percents all the time. <<Announcer voice>> “Jones is only shooting
- 00:06
27 percent from the field tonight.” Field goal and free throw accuracy in basketball,
- 00:07
batting averages in baseball, passing completion rates in football… are all expressed in
- 00:07
percents. We hope your knowledge of percents has now
- 00:08
been improved by at least 62%. In fact, you even look 62% smarter than when
- 00:08
we started… But wait… there’s more!
- 00:08
You know that rare, valuable painting you found in the attic?
- 00:12
The one of all the trees? Well, apparently some collectors really like trees, because
- 00:16
it’s now worth $45,055. That is some fancy foliage.
- 00:26
Thank goodness you didn’t uncover it five years ago and sell it back then.
- 00:31
Now that we mention it… how much could you have sold it for five years ago?
- 00:38
Well, the painting’s value is appreciating annually by 15%.
- 00:47
So… how much would it have been worth half a decade earlier?
- 00:54
A - $10,265 B - $19,990
- 00:56
C - $21,780 D - $22,400
- 00:57
or E - $34,210? First, we’re going to need to pull a variable
- 01:02
out of our bag of tricks. Let’s make “V” the value of the painting
- 01:09
five years ago. Because we have the appreciated value and
- 01:13
want to find the original value, we should set our equation like this:
- 01:18
45,055 equals V times one plus point-one-five to the fifth.
- 01:24
Whoa – how did we get there? Well, the value of the painting increases
- 01:29
by 15% every year… …which is the “one plus point-one-five.”
- 01:34
The value is multiplied by that amount – one-point-one-five – for every year that passes.
- 01:41
So it’s the same as V times 1.15 times 1.15 times 1.15 times 1.15 times 1.15.
- 01:53
Okay, but our V is crowded with a whole mix of junk on the right side of the equation.
- 02:02
We want to get it by itself, so we can reconfigure the equation to look like this:
- 02:06
V equals 45,055 divided by 1.15 to the fifth. Then it’s simply a matter of doing the math…
- 02:30
or politely asking your calculator to do it for you
- 02:32
. Implore your calculator to first take 1.15
- 02:39
to the fifth… ...and then divide 45,055 by that result.
- 03:00
So looks like V equals $22,400.29. After dropping those 29 cents into your math
- 03:11
teacher’s tip jar, it appears our answer is option D.
- 03:18
Wow – it’s already worth nearly $23,000 more than it was five years ago!
- 03:22
At this rate, you’ll be able to retire in a few decades.
- 03:26
Assuming your future kids don’t one day try to add a few more trees.
Related Videos
SAT Math 10.3 Geometry and Measurement. What is the ratio of birds to dogs?
SAT Math 2.1 Statistics and Probability. Which two items have the highest protein to fat ratio?
SAT Math 2.2 Statistics and Probability. What percent of her recommended daily intake of 2000 calories did she consume?