Reimann Sum:
The Reimann Sum of a function
f (
x) over an interval [
a,
b] is defined as
where
xi-1 <
xi* <
xi, and
xi, and for
i = 1,…
n divides the interval [
a,
b] into
n subintervals.
Left Hand Sum:
The Left-Hand Sum of a function f (x) over an interval [a, b] is defined as  where xi for i = 1,…,n divides the interval [a, b] into n subintervals.
where xi for i = 1,…,n divides the interval [a, b] into n subintervals.Right Hand Sum:
The Right-Hand Sum of a function f (x) over an interval [a, b] is defined as  where xi for i = 1,…,n divides the interval [a, b] into n subintervals.
where xi for i = 1,…,n divides the interval [a, b] into n subintervals.Midpoint Sum:
The Midpoint Sum of a function f (x) over an interval [a,b] is defined as  where
where  , and xi for i = 1,…,n divides the interval [a, b] into n subintervals.
, and xi for i = 1,…,n divides the interval [a, b] into n subintervals.Trapezoid Sum:
Trapezoid sum is the average between the Left Hand and Right Hand Sum.
Average Value Of A Function:
The average value of a continuous function
f on the closed interval [
a,
b] is defined as
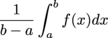
.
Concavity:
This describes whether the function is curving up, down or not curving at all.
Critical Point:
The derivative of the function at the critical point is 0.
Inflection Point:
The point (
x-value) where the function changes concavity.
Secant Line:
The line joining two points on the graph of a function.
Tangent Line:
A line that touches the graph of a function
f (
x) at a point.
Differentiability:
If the limit exists, the function
f (
x) is differentiable at
x =
a.
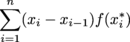 where xi-1 < xi* < xi, and xi, and for i = 1,…n divides the interval [a, b] into n subintervals.
where xi-1 < xi* < xi, and xi, and for i = 1,…n divides the interval [a, b] into n subintervals. where xi for i = 1,…,n divides the interval [a, b] into n subintervals.
where xi for i = 1,…,n divides the interval [a, b] into n subintervals.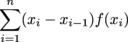 where xi for i = 1,…,n divides the interval [a, b] into n subintervals.
where xi for i = 1,…,n divides the interval [a, b] into n subintervals.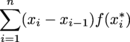 where
where 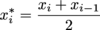 , and xi for i = 1,…,n divides the interval [a, b] into n subintervals.
, and xi for i = 1,…,n divides the interval [a, b] into n subintervals.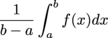 .
.