Fundamental Theorem Of Calculus
This theorem provides a relation between the derivative and the definite integral of a function.

Second Fundamental Theorem Of Calculus
This theorem provides a method of differentiating an integral.

Integration By Parts
A technique for performing integration where 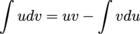 .
.Improper Integral
An definite integral 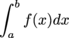 is called an improper integral when the limits of integration are infinite (a = -∞, b = ∞) or the function becomes unbounded in [a, b].
is called an improper integral when the limits of integration are infinite (a = -∞, b = ∞) or the function becomes unbounded in [a, b].Reimann Sum
The Reimann Sum of a function f(x) over an interval [a, b] is defined as 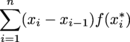 where xi-1 < xi* < xi, and xi for i = 1,…,n divides the interval [a, b] into n subintervals.
where xi-1 < xi* < xi, and xi for i = 1,…,n divides the interval [a, b] into n subintervals.Left-Hand Sum
The Left-Hand Sum of a function f(x) over an interval [a, b] is defined as  where xi for i = 1,…,n divides the interval [a, b] into n subintervals.
where xi for i = 1,…,n divides the interval [a, b] into n subintervals.Right-Hand Sum
The Right-Hand Sum of a function f ( x ) over an interval [a,b] is defined as 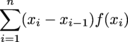 where xi for i = 1,…,n divides the interval [a,b] into n subintervals.
where xi for i = 1,…,n divides the interval [a,b] into n subintervals.Midpoint Sum
The Midpoint Sum of a function
f (
x) over an interval [
a,
b] is defined as
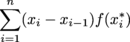
where
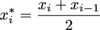
, and
xi for
i = 1,…,
n divides the interval [
a,
b] into
n subintervals.
Trapezoid Sum
The trapezoid sum is the average between the Left-Hand and Right-Hand Sum.
Average Value Of A Function
Average value of a continuous function f on the closed interval [a, b] is defined as 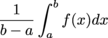
.
Concavity
This describes whether the function is curving up, down or not curving at all.
Critical Point
The derivative of the function at the critical point is 0.
Inflection Point
The point (
x-value) where the function changes concavity.
Secant Line
A line joining two points on the graph of a function.
Tangent Line
A line that touches the graph of a function
f (
x) at a point.
Differentiability
If the limit
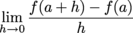
exists, the function
f (
x) is differentiable at
x =
a.


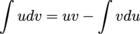 .
.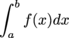 is called an improper integral when the limits of integration are infinite (a = -∞, b = ∞) or the function becomes unbounded in [a, b].
is called an improper integral when the limits of integration are infinite (a = -∞, b = ∞) or the function becomes unbounded in [a, b].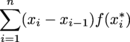 where xi-1 < xi* < xi, and xi for i = 1,…,n divides the interval [a, b] into n subintervals.
where xi-1 < xi* < xi, and xi for i = 1,…,n divides the interval [a, b] into n subintervals. where xi for i = 1,…,n divides the interval [a, b] into n subintervals.
where xi for i = 1,…,n divides the interval [a, b] into n subintervals.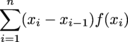 where xi for i = 1,…,n divides the interval [a,b] into n subintervals.
where xi for i = 1,…,n divides the interval [a,b] into n subintervals.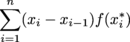 where
where 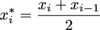 , and xi for i = 1,…,n divides the interval [a, b] into n subintervals.
, and xi for i = 1,…,n divides the interval [a, b] into n subintervals.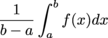 .
.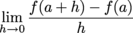 exists, the function f (x) is differentiable at x = a.
exists, the function f (x) is differentiable at x = a.