We can't figure out the value of ∠KMN directly; those trig ratios only work for right triangles. Instead, we'll have to be sneaky about it. Since ∠KMN is part of a larger angle, subtracting ∠LMK from ∠LMN should give us the right value. m∠KMN = m∠LMN – m∠LMK Focusing on the first angle, ∠LMN, we know the hypotenuse and the adjacent side. Since it's the angle we're looking for, that translates to inverse cosine.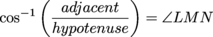 
Add in what we know.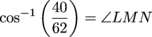 
Plugging it into our calculator gives us: ∠LMN ≈ 49.8° We're off to a great start. The second angle is going to be a bit trickier. Before we can calculate m∠LMK, we'll need to know something else about the smaller right triangle. Since the unknown leg LK is half of the larger right triangle's leg LN, we can start by finding LN. The Pythagorean Theorem would work just as well, but we'll stick to trig.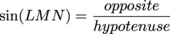 
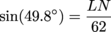
Rearrange to solve for LN. LN = 62sin(49.8°)
LN ≈ 47.4 Great, but we were actually looking for LK. Dividing LN by 2 will give us LK.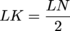 
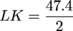
LK = 23.7 Wonderful. The whole point of calculating LK was so we could find ∠LMK. Now with both the legs of ∆LKM found, we can use the inverse tangent to find ∠LMK. 
Remember, we're looking at the smaller triangle with respect to ∠LMK. That means our opposite side is LK and our adjacent side is ML.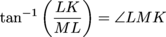 
Substitute in those values and solve.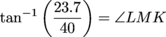 
∠LMK ≈ 30.7° Finding ∠KMN hasn't been an easy task, but now that we know ∠LMN and ∠LMK, we can do it. Finally. m∠KMN = m∠LMN – m∠LMK Plug in our values. ∠KMN = 49.8° – 30.7°
∠KMN = 19.1° | 
) and/or looking at the grid can give us the lengths of the legs of the triangle. 
